Der rechnerische Zusammenhang: GM = g * r² zeigt, dass das Produkt: G * Masse eine Raumgröße darstellt.
Diese Raumgröße ist unabhängig von r bei allen Berechnungen zur Gravitationsbeschleunigung stets gleich groß. Je kleiner r ist, desto
größer ist g.
r bezieht sich dabei nicht auf den Planetenradius selber, sondern auf die kugelförmige Ausbreitung der Gravitationswirkung vom
Massenzentrum des Planeten, also auf den konkreten Abstand eines Probekörpers zu diesem Massezentrum.
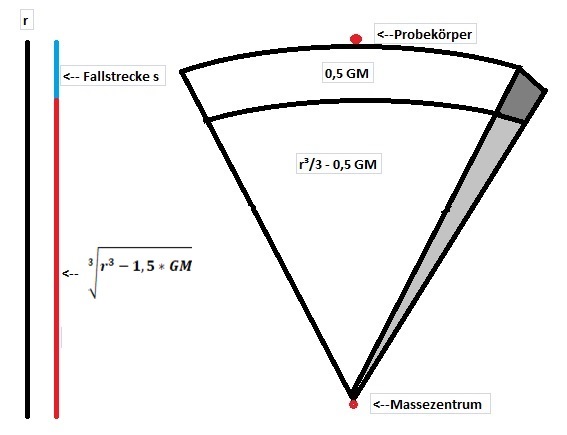
Der gesamte Beschleunigungsraum eines Probekörpers bis hin zum Massenzentrum des Planeten ist dabei als eine Pyramide anzusehen,
deren Grundfläche: r² auf der Höhe des Probekörpers liegt und deren Spitze am Massenzentrum des Planeten anliegt. GM stellt dabei den
Teil dieses Beschleunigungsraumes dar, den der Probekörper beim Fall hin zum Massenzentrum während einer Sekunde durchquert.
Der gesamte Beschleunigungsraum beträgt als Pyramidenvolumen also: r³/3. Von diesem ist die Raumgröße GM abzuziehen.
Mit der Kubikwurzel aus dem 3-fachen dieser Differenz wäre dann der Rest der Beschleunigungsstrecke nach einer Sekunde zu ermitteln.
Da jedoch die schrittweise Zunahme der Beschleunigung pro Sekunde nicht von der Beschleunigungsstrecke abhängt, sondern von der
konkreten Fallstrecke, ist die Berechnung umzukehren: Es muss zunächst die Fallstrecke berechnet werden, um dann von dieser auf
den korrekten Beschleunigungswert hochzurechnen.
Für die Fallstrecke ist die Hälfte des Beschleunigungsraumes je Sekunde (GM) anzusetzen:


Die Fallstrecke selber ergibt sich damit aus dem Abzug dieses Ergebnisses von r.
Erweitert um die Falldauer t ist diese Berechnung auf jeden Fallprozess unabhängig von seiner Dauer anwendbar:
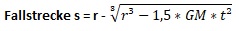
Daraus errechnet sich dann die über die Fallstrecke hin durchschnittliche Beschleunigung a mit: a = s/(0,5*t²) bzw. a = 2*s/t²
Alternativ und die tatsächlichen Verhältnisse noch besser widerspiegelnd kann die Berechnung auch auf der Basis des gesamten
Kugelvolumens eines Beschleunigungsraumes erfolgen:
Dabei bildet jedoch die gesamte Kugeloberfläche die Basisfläche dieses Raumes: GM ist um den Faktor 4*Pi zu erweitern:
G * 4 * Pi = 8,38714760640051E-10 m³/(kg * sek²)
GM * 4 * Pi = 5,008960879E+15 m³/sek²
Der gesamte Beschleunigungsraum V berechnet sich dann auf: 4/3 * Pi * r³ = 1,08320731979674E+21 m³ (hier ist r = durchschn. Erdradius).
Davon abzuziehen ist 0,5 * GM * 4 * Pi: der Rest-Beschleunigungsraum V' nach einer Sekunde Fallstrecke beträgt dann
1,0832048153163E+21 m³.
Daraus ist der Radius von V' zu ermitteln mit:
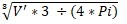 = 6.370.995,87987218 m.
= 6.370.995,87987218 m.Die Differenz zu r ergibt dann die Fallstrecke: 4,91012781672179 m für eine Sekunde Falldauer. (Vergleiche zum Ergebnis in Kap. 1)
Dieses Verfahren mag zur Überprüfung der zuvor entwickelten Formeln dienen, in der Praxis wäre die Wertumstellung von G sowie
das umständlichere Berechnungsverfahren jedoch wenig tauglich.